length contraction

Observers moving uniformly in unified space-time in relation to objects calculate that object length in uniform-velocity direction is shorter than for relatively stationary objects {distance contraction} {length contraction}|.

relativity

Stationary observers calculate that moving objects have shorter lengths in movement direction than stationary objects. Moving observers calculate that stationary objects are moving and have shorter lengths in movement direction. In both cases, observer and object have relative velocity. See Figure 1.

direction

Length contraction happens only in movement direction. Length contraction depends on relative transverse velocity. The radial velocity component has no effect, and directions perpendicular to movement direction have no length contraction.

distance from observer

Because contraction direction is perpendicular to distance direction, distance away does not affect length-contraction ratio.

calculation

When stationary observers look at moving rulers, ruler points do not have same time. See Figure 1.

space-time reference frame

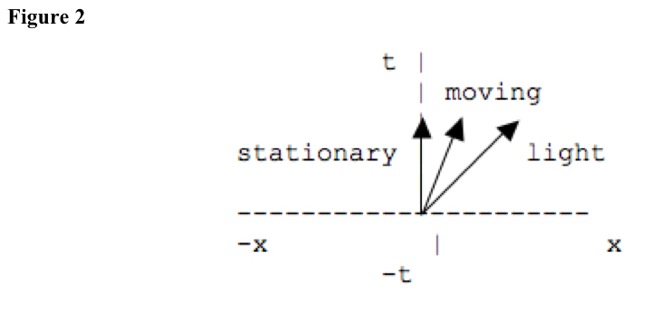
On space-time reference frames, moving events trace vectors. Stationary objects trace vectors parallel to time coordinate. See Figure 2.

space-time separation

Space-time events are separate in both time and space.

Compared to stationary rulers, moving-ruler leading end is earlier in time and behind in space. Trailing end is later in time and ahead in space. Observer calculates that object length and time are shorter. Length contraction and time dilation have same percentage, so physical laws do not change, and space-time separation is same as before. For all uniformly moving observers, physical laws are the same, and space-time separations are the same.

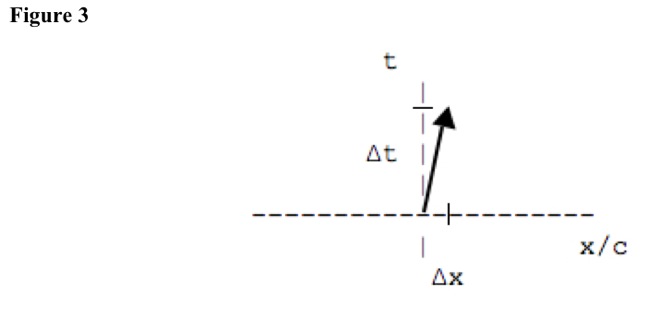
See Figure 3. In space-time, space gain causes time loss, so space-time separation s depends on space separation x and time separation t (ignoring y and z dimensions). Because distance x is light speed c times time t, s^2 = x^2 - (c*t)^2, using distance units, or s^2 = t^2 - x^2/c^2, using time units.

For constant motion, t = x/v, so s^2 = (x/v)^2 - (x/c)^2 = x^2 * (1/v^2 - 1/c^2) = (x^2 / v^2) *(v^2 / v^2 - v^2 / c^2) = (x^2 / v^2) * (1 - v^2 / c^2) = (x^2 / c^2) * (c^2 - v^2) / v^2. Therefore, s = (x/v) * (1 - v^2 / c^2)^0.5 or s = (x/c) * (c^2 - v^2)^0.5 / v. Stationary observers calculate that moving-object length is shorter than stationary length.

length-contraction percentage

If moving object has velocity 0.5 * c (half light speed), space-time separation s = (x/c) * (((c^2 - 0.5 * c)^2)^0.5 / (0.5 * c)) = (x/c) * ((c^2 - 0.25 * c^2)^0.5 / (0.5 * c)) = (x/c) * ((0.75*c^2)^0.5 / (0.5 * c)) = (x/c) * 0.865/0.5 = 0.43 * (x/c).

If moving object has velocity 0.9 * c (nine-tenths light speed), space-time separation s = (x/c) * ((c^2 - (0.9 * c)^2)^0.5 / (0.9 * c)) = (x/c) * 0.19/0.9 = 0.21 * (x/c).

If moving object has velocity 0.99 * c (99% light speed), space-time separation s = (x/c) * ((c^2 - (0.99 * c)^2)^0.5 / (0.99 * c)) = (x/c) * 0.02/0.99 = 0.02 * (x/c).

As moving object approaches light speed, stationary observer sees that length decreases toward zero. Stationary objects have maximum space-time separation.

maximum speed

Length less than zero is impossible. Therefore, nothing can go faster than light speed, and nothing can go backward in time.

length measurement

To measure stationary rulers, stationary observers at one ruler end can send signals to a reflector at other end. See Figure 4. Signal travels from end to end and back. Time to go is same as time to return. Travel time is directly proportional to length.

To measure moving rulers, stationary observers at one ruler end can send signals to a reflector at other end. Ruler reflector moves closer as signal travels and reflects earlier. Observer measures shorter time and measures that ruler has shorter length.

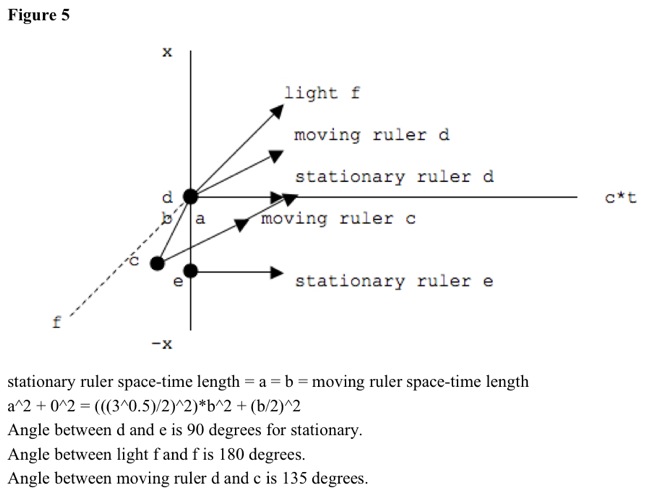
Stationary observers calculate that stationary rulers spread over space only. Stationary observers calculate that moving rulers spread over space and time. Stationary and moving rulers have same space-time separation. See Figure 5.

For moving rulers, for ends to seem simultaneous, ends lie along line tilted away from vertical, not on vertical. See Figure 5. Leading end is further along in space, and trailing end is behind in space. Middle moves toward where leading end was, and away from where trailing end was. For signals to reach middle simultaneously, leading end must signal later in time, and trailing end must signal earlier in time.

time

When moving object passes stationary observer, one end reaches observer before other end. Other end lags behind in time, because ends are traveling through time at less than light speed, and it takes time for other end to reach observer. When moving object moves through space faster, lengths appear shorter, and moving object moves through time slower, so time slows. See Figure 2. At less than light speed, angle is less than 45 degrees. At light speed, angle is 45 degrees.

analogies

Length contraction is like looking at rulers rotated away from perpendicular to sightline. For space-time, rotation is into time dimension.

Length contraction is like looking at rulers from farther away.

Length contraction is like light rays curving inward from both ruler ends, like a concave lens (opposite from gravitational lensing).

Because space-time separation has a negative sign under the square root, length contraction is like using imaginary numbers. Space-time time coordinate is like imaginary axis, so space-time is like complex plane.